Resumen
Al realizar este laboratorio se comprueba a través de la experimentación el movimiento uniforme y uniformemente acelerado. Esto se demuestra, haciendo uso de las graficas; la relación entre espacio recorrido y tiempo empleado por una partícula, se busca comprobar que para el movimiento uniforme, en cada intervalo de tiempo la velocidad es constante, contraria al movimiento uniformemente acelerado donde a través del experimento se demuestra que la velocidad aumenta proporcionalmente respecto al tiempo. Con los resultados obtenidos a través del experimento se demostrará la valides de las ecuaciones cinemáticas con el fin de afianzar dicho conocimiento, para esto se utiliza el riel de aire donde se simulan los dos movimientos y se toman los datos de espacio y tiempo a través de unos sensores ópticos conectados a un contador, para realizar con estos los respectivos cálculos que demuestran la teoría una vez más.
TEORÍA RELACIONADA
SISTEMAS DE REFERENCIA INERCIALES.
En mecánica se dice que un sistema de referencia es un sistema de referencia inercial cuando las leyes del movimiento cumplen la conservación del Momento lineal. El término aparece principalmente en mecánica newtoniana donde los sistemas inerciales son precisamente aquellos en los que se cumplen las leyes de Newton [1].
Las características de los sistemas inerciales son:
El punto de referencia es arbitrario, dado un sistema de referencia inercial, cualquier otro sistema desplazado respecto al primero una distancia fija sigue siendo inercial (el espacio es homogéneo).
La orientación de los ejes es arbitraria, dado un sistema de referencia inercial otro sistema de referencia, con otra orientación distinta del primero, sigue siendo inercial (el espacio es isotrópico).
Las características de los sistemas inerciales son:
El punto de referencia es arbitrario, dado un sistema de referencia inercial, cualquier otro sistema desplazado respecto al primero una distancia fija sigue siendo inercial (el espacio es homogéneo).
La orientación de los ejes es arbitraria, dado un sistema de referencia inercial otro sistema de referencia, con otra orientación distinta del primero, sigue siendo inercial (el espacio es isotrópico).
Desplazamiento a velocidad lineal constante, dado un sistema de referencia inercial cualquier, otro que se desplace con velocidad lineal y constante, sigue siendo inercial.
Por combinación de los tres casos anteriores, tenemos que cualquier sistema de referencia desplazado respecto a uno inercial, girado y que se mueva a velocidad lineal y constante, sigue siendo inercial [1].
Por combinación de los tres casos anteriores, tenemos que cualquier sistema de referencia desplazado respecto a uno inercial, girado y que se mueva a velocidad lineal y constante, sigue siendo inercial [1].
MOVIMIENTO RECTILINEO.
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta; En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen [2]. Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando

O gráficamente, en la representación de v en función de t.
 Grafica1. Velocidad versus tiempo en el movimiento uniforme.
Grafica1. Velocidad versus tiempo en el movimiento uniforme.Habitualmente, el instante inicial t0 se toma como cero, por lo que las ecuaciones del movimiento uniforme resultan
 Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v0 entre los instantes t0 y t, mediante integración, o gráficamente [2].
Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v0 entre los instantes t0 y t, mediante integración, o gráficamente [2].
 Grafica 2. Aceleración versus tiempo en el movimiento uniformemente acelerado.
Grafica 2. Aceleración versus tiempo en el movimiento uniformemente acelerado.Dada la velocidad en función del tiempo, obtenemos el desplazamiento x-x0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando [2]

 Grafica 3. Velocidad versus tiempo en el movimiento uniformemente acelerado.
Grafica 3. Velocidad versus tiempo en el movimiento uniformemente acelerado.Habitualmente, el instante inicial t0 se toma como cero, quedando las fórmulas del movimiento rectilíneo uniformemente acelerado, las siguientes. [2]

Despejando el tiempo t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad v con el desplazamiento x-x0
 VELOCIDAD INSTANTANEA.
VELOCIDAD INSTANTANEA.La velocidad media entre los instantes t y t' está definida por

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Δt tan pequeño como sea posible, en el límite cuando Δt tiende a cero.

Pero dicho límite, es la definición de derivada de x con respecto del tiempo t [2].
ACELERACION INSTANTANEA.
En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t.
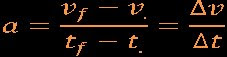
La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que es la definición de la derivada de v. [2] 
Para realizar este laboratorio el profesor primero realiza la explicación de las ecuaciones cinemáticas tanto para el movimiento rectilíneo uniforme y el movimiento rectilíneo uniformemente acelerado, donde se muestra la forma de obtenerla matemáticamente. Realizada la explicación se procede a realizar el experimento con el riel de aire, primero se toma datos para el movimiento rectilíneo uniforme, se proporciona aire al riel por medio de un tuvo de presión conectado a un soplador. Sobre el riel se debe colocar un deslizador y sobre este un diafragma de longitud de 100mm, se colocan 5 barreras ópticas alineadas con relación al riel donde se mide la distancia entre las barreras, estas a su vez están conectadas a un contador 4-4, que mide en el modo uno, el tiempo que dura el diafragma en pasar por la primera barrera, que es el punto de referencia y a la vez coloca a funcionar el contador; luego éste pasa por cada barrera parando los cronómetros, de aquí se obtuvo el tiempo que demora desde el punto de referencia a cada una de las barrera. El deslizador es lanzado por un disparador para que pase por dichas barreras, estos datos de tiempo son tomados para su posterior análisis.
Para tomar los segundos datos se coloca el contador en el modo dos y se lanza el deslizador ara que le diafragma pase a través de los sensores, el tiempo medido por los sensores es el que demora el diafragma en pasar por el sensor, estos datos son anotados.Para el movimiento rectilíneo uniformemente acelerado se realiza el mismo montaje con el riel, pero esta vez se coloca un hilo amarado al deslizador y se pasa a través de una polea de precisión que se encuentra ajustada al extremo final del riel, el hilo sostiene amarrado un porta pesas y se le coloca una masa aceleradora, se invierte el disparador para que este en vez de impulsarlo, libere al deslizador. Éste a su vez comienza a moverse por la masa aceleradora que pende de él, se coloca el contador en modo uno y se deja correr nueva mente el deslizador así se toman los datos, esto se realiza una vez para cada modo, el montaje se muestra en la figura 1.
 Figura 1. Montaje realizado para realizar el laboratorio del movimiento rectilíneo.
Figura 1. Montaje realizado para realizar el laboratorio del movimiento rectilíneo.
 Tabla 1: distancia recorrida por el deslizador con el diafragma instalado sobre él y donde se localiza cada sensor en el movimiento rectilíneo uniforme.
Tabla 1: distancia recorrida por el deslizador con el diafragma instalado sobre él y donde se localiza cada sensor en el movimiento rectilíneo uniforme.
 Tabla 2. Datos de tiempo tomados en el modo 1 del contador 4-4 para el movimiento rectilíneo que indican el tiempo que demora en llegar el deslizador con el diafragma puesto, desde el punto de referencia (primer sensor) a las demás distancias medidas a cada sensor.
Tabla 2. Datos de tiempo tomados en el modo 1 del contador 4-4 para el movimiento rectilíneo que indican el tiempo que demora en llegar el deslizador con el diafragma puesto, desde el punto de referencia (primer sensor) a las demás distancias medidas a cada sensor.
 Tabla 3. Datos de tiempo tomados en el modo 2 del contador 4-4 para el movimiento rectilíneo uniforme que indican el tiempo que demora en pasar el diafragma por cada uno de los sensores.
Tabla 3. Datos de tiempo tomados en el modo 2 del contador 4-4 para el movimiento rectilíneo uniforme que indican el tiempo que demora en pasar el diafragma por cada uno de los sensores.
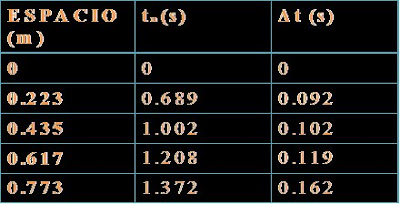 Tabla 4. Distancias recorrida por deslizador, datos de tiempo medidos en modo 1 del contador 4-4 que indica el tiempo que demora en llegar el deslizador desde e punto de referencia (primer sensor) a las demás distancias medidas a cada sensor
Tabla 4. Distancias recorrida por deslizador, datos de tiempo medidos en modo 1 del contador 4-4 que indica el tiempo que demora en llegar el deslizador desde e punto de referencia (primer sensor) a las demás distancias medidas a cada sensor
Tn Y datos de tiempo tomados en el modo 2 en el movimiento rectilíneo uniformemente acelerado indican el tiempo que demora el deslizador pasando por el sensor Δt.
1) Para cuando el deslizador se movía con velocidad constante.Realice las graficas: espacio recorrido en función del tiempo la velocidad en función del tiempo. Determine la mejor curva en cada caso; para realizar la grafica de velocidad en función del tiempo utilice los siguientes tiempos :

R/ a) para realizar la siguiente grafica se realiza el espacio medido contra tn porque representan el tiempo que demora el deslizador en llegar a cada sensor.
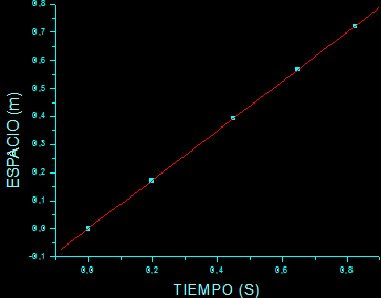 Grafica 4: espacio recorrido versus tiempo para deslizador con movimiento uniforme.
Grafica 4: espacio recorrido versus tiempo para deslizador con movimiento uniforme.
De la regresión a la grafica anterior se obtiene la siguiente ecuación:

b) Para realizar la grafica de la velocidad en función del tiempo se utiliza la ecuación :



 Grafica 5: velocidad versus tiempo del deslizador con movimiento uniforme.
Grafica 5: velocidad versus tiempo del deslizador con movimiento uniforme.


MONTAJE Y PROCEDIMIENTO
Para realizar este laboratorio el profesor primero realiza la explicación de las ecuaciones cinemáticas tanto para el movimiento rectilíneo uniforme y el movimiento rectilíneo uniformemente acelerado, donde se muestra la forma de obtenerla matemáticamente. Realizada la explicación se procede a realizar el experimento con el riel de aire, primero se toma datos para el movimiento rectilíneo uniforme, se proporciona aire al riel por medio de un tuvo de presión conectado a un soplador. Sobre el riel se debe colocar un deslizador y sobre este un diafragma de longitud de 100mm, se colocan 5 barreras ópticas alineadas con relación al riel donde se mide la distancia entre las barreras, estas a su vez están conectadas a un contador 4-4, que mide en el modo uno, el tiempo que dura el diafragma en pasar por la primera barrera, que es el punto de referencia y a la vez coloca a funcionar el contador; luego éste pasa por cada barrera parando los cronómetros, de aquí se obtuvo el tiempo que demora desde el punto de referencia a cada una de las barrera. El deslizador es lanzado por un disparador para que pase por dichas barreras, estos datos de tiempo son tomados para su posterior análisis.
Para tomar los segundos datos se coloca el contador en el modo dos y se lanza el deslizador ara que le diafragma pase a través de los sensores, el tiempo medido por los sensores es el que demora el diafragma en pasar por el sensor, estos datos son anotados.Para el movimiento rectilíneo uniformemente acelerado se realiza el mismo montaje con el riel, pero esta vez se coloca un hilo amarado al deslizador y se pasa a través de una polea de precisión que se encuentra ajustada al extremo final del riel, el hilo sostiene amarrado un porta pesas y se le coloca una masa aceleradora, se invierte el disparador para que este en vez de impulsarlo, libere al deslizador. Éste a su vez comienza a moverse por la masa aceleradora que pende de él, se coloca el contador en modo uno y se deja correr nueva mente el deslizador así se toman los datos, esto se realiza una vez para cada modo, el montaje se muestra en la figura 1.
 Figura 1. Montaje realizado para realizar el laboratorio del movimiento rectilíneo.
Figura 1. Montaje realizado para realizar el laboratorio del movimiento rectilíneo.RESULTADOS
Los siguientes datos de longitud tienen una incertidumbre de ± 1mm y los de tiempo de ± 0.001s.
DATOS MEDIDOS PARA EL MOVIMIENTO RECTILINEO UNIFORME
 Tabla 1: distancia recorrida por el deslizador con el diafragma instalado sobre él y donde se localiza cada sensor en el movimiento rectilíneo uniforme.
Tabla 1: distancia recorrida por el deslizador con el diafragma instalado sobre él y donde se localiza cada sensor en el movimiento rectilíneo uniforme. Tabla 2. Datos de tiempo tomados en el modo 1 del contador 4-4 para el movimiento rectilíneo que indican el tiempo que demora en llegar el deslizador con el diafragma puesto, desde el punto de referencia (primer sensor) a las demás distancias medidas a cada sensor.
Tabla 2. Datos de tiempo tomados en el modo 1 del contador 4-4 para el movimiento rectilíneo que indican el tiempo que demora en llegar el deslizador con el diafragma puesto, desde el punto de referencia (primer sensor) a las demás distancias medidas a cada sensor. Tabla 3. Datos de tiempo tomados en el modo 2 del contador 4-4 para el movimiento rectilíneo uniforme que indican el tiempo que demora en pasar el diafragma por cada uno de los sensores.
Tabla 3. Datos de tiempo tomados en el modo 2 del contador 4-4 para el movimiento rectilíneo uniforme que indican el tiempo que demora en pasar el diafragma por cada uno de los sensores.DATOS MEDIDOS PARA EL MOVIMIENTO RECTILINEO UNIFORMEMENTE ACELERADO
 Tabla 4. Distancias recorrida por deslizador, datos de tiempo medidos en modo 1 del contador 4-4 que indica el tiempo que demora en llegar el deslizador desde e punto de referencia (primer sensor) a las demás distancias medidas a cada sensor
Tabla 4. Distancias recorrida por deslizador, datos de tiempo medidos en modo 1 del contador 4-4 que indica el tiempo que demora en llegar el deslizador desde e punto de referencia (primer sensor) a las demás distancias medidas a cada sensorTn Y datos de tiempo tomados en el modo 2 en el movimiento rectilíneo uniformemente acelerado indican el tiempo que demora el deslizador pasando por el sensor Δt.
ANÁLISIS Y CONCLUSIONES
1) Para cuando el deslizador se movía con velocidad constante.Realice las graficas: espacio recorrido en función del tiempo la velocidad en función del tiempo. Determine la mejor curva en cada caso; para realizar la grafica de velocidad en función del tiempo utilice los siguientes tiempos :

R/ a) para realizar la siguiente grafica se realiza el espacio medido contra tn porque representan el tiempo que demora el deslizador en llegar a cada sensor.
 Grafica 4: espacio recorrido versus tiempo para deslizador con movimiento uniforme.
Grafica 4: espacio recorrido versus tiempo para deslizador con movimiento uniforme.De la regresión a la grafica anterior se obtiene la siguiente ecuación:

b) Para realizar la grafica de la velocidad en función del tiempo se utiliza la ecuación :


Donde; x = longitud del diafragma, Δt = tiempo registrados en el modo 2 (Δt) para el movimiento uniforme.

Como nos podemos dar cuenta la velocidad es constante puesto que los cuatro valores calculados de la velocidad fueron equivalentes. Para graficar la velocidad en función del tiempo se escoge la moda que fue el valor de 0.862s
 Grafica 5: velocidad versus tiempo del deslizador con movimiento uniforme.
Grafica 5: velocidad versus tiempo del deslizador con movimiento uniforme.2. Con base en las graficas anteriores responda: ¿Cómo se relacionan el espacio recorrido y el tiempo en el movimiento rectilíneo uniforme? ¿Qué significado tiene la pendiente de esta grafica? ¿Cómo se relacionan la velocidad y el tiempo en el movimiento rectilíneo uniforme? ¿Qué significado físico tiene el área bajo esta grafica?
R/ a) El espacio recorrido y el tiempo empleado en el movimiento uniforme son magnitudes directamente proporcionales, al aumentar una la otra aumenta en la misma proporción. Como estas magnitudes son directamente proporcionales están ligadas por un cociente constante que es la velocidad, matemáticamente se puede expresar de la siguiente manera:

Analizando dimensionalmente: Por sus dimensiones la constate k se mide m/s que es la razón de cambio de la posición del deslizador con respecto al tiempo (velocidad) y esta a su vez es contante, es decir, que no hay aceleración.
Por sus dimensiones la constate k se mide m/s que es la razón de cambio de la posición del deslizador con respecto al tiempo (velocidad) y esta a su vez es contante, es decir, que no hay aceleración.


 Por sus dimensiones la constate k se mide m/s que es la razón de cambio de la posición del deslizador con respecto al tiempo (velocidad) y esta a su vez es contante, es decir, que no hay aceleración.
Por sus dimensiones la constate k se mide m/s que es la razón de cambio de la posición del deslizador con respecto al tiempo (velocidad) y esta a su vez es contante, es decir, que no hay aceleración.b) El significado físico de la pendiente de la grafica 4 en el movimiento uniforme representa la variación de la posición de la partícula con respecto al tiempo. Esto indica que es la velocidad, para este caso medida en m/s.
c) La velocidad y el tiempo se relacionan según la grafica 5 de forma constante, esto quiere decir que esta no cambia su magnitud y dirección con respecto al tiempo, gráficamente se obtiene como resultado una línea paralela al eje del tiempo, lo que indica que no hay aceleración.
d) El significado físico el área bajo la grafica representa el espacio recorrido por la partícula. Matemáticamente no es más que la integral de la velocidad con respecto al tiempo.
d) El significado físico el área bajo la grafica representa el espacio recorrido por la partícula. Matemáticamente no es más que la integral de la velocidad con respecto al tiempo.

3. Para cuando el deslizador se movía con aceleración constate. Realice las graficas: espacio recorrido en función del tiempo y velocidad en función del tiempo. Determine la mejor curva en cada caso; para realizar la grafica de velocidad en función del tiempo utilice los siguientes tiempos:

R/ a) Grafica 6: espacio versus tiempo del deslizador con movimiento uniformemente acelerado.
Grafica 6: espacio versus tiempo del deslizador con movimiento uniformemente acelerado.

 Grafica 6: espacio versus tiempo del deslizador con movimiento uniformemente acelerado.
Grafica 6: espacio versus tiempo del deslizador con movimiento uniformemente acelerado.La ecuación obtenida de la regresión realizada a la grafica de espacio versus tiempo para cuando el deslizador se movía con movimiento uniformemente acelerado:

b)
 se utiliza esta ecuación del movimiento uniforme aunque el movimiento es acelerado por que se requiere la velocidad en un intervalo de de espacio muy pequeño que es la longitud del diafragma del deslizador equivalente a 0.100 m en le momento de pasar por el sensor óptico en este intervalo de tiempo tan pequeño la variación de la velocidad casi es nula lo que hace que el movimiento sea aproximadamente con velocidad constante por esto se hace esta aproximación.
se utiliza esta ecuación del movimiento uniforme aunque el movimiento es acelerado por que se requiere la velocidad en un intervalo de de espacio muy pequeño que es la longitud del diafragma del deslizador equivalente a 0.100 m en le momento de pasar por el sensor óptico en este intervalo de tiempo tan pequeño la variación de la velocidad casi es nula lo que hace que el movimiento sea aproximadamente con velocidad constante por esto se hace esta aproximación.
Se utiliza el tiempo medido en modo 2

 Grafica 7: velocidad versus tiempo del deslizador con movimiento uniforme acelerado.
Grafica 7: velocidad versus tiempo del deslizador con movimiento uniforme acelerado.
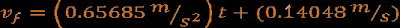
R/ a) En la grafica de espacio versus tiempo se obtuvo una parábola lo que indican que estas magnitudes no son directamente proporcionales puesto que la pendiente de la grafica que es físicamente la velocidad no es una línea recta lo que indica que la velocidad varía respecto al tiempo y que lo hace de forma proporcional puesto que curva presenta que dicho movimiento se define matemáticamente con una ecuación de segundo grado:

b) La pendiente de esta grafica representa la velocidad del móvil el cual esta medida en m/s y va cambiando al transcurrir el tiempo lo que indica que hay una aceleración.
c) de la grafica 7 se puede deducir que la velocidad y el tiempo son dos magnitudes directamente proporcionales en el movimiento uniformemente acelerado lo que indica que al aumentar una la otra aumenta en al misma proporción.
 indica que la velocidad varia linealmente en el tiempo, este es el significado físico del área bajo la pendiente de la grafica velocidad versus tiempo. Matemáticamente:
indica que la velocidad varia linealmente en el tiempo, este es el significado físico del área bajo la pendiente de la grafica velocidad versus tiempo. Matemáticamente:

R/ Los errores se dieron porque los alumnos movían el riel de aire desnivelándolo, resultando discrepancia en los datos de tiempo tomados. Esto se corregiría si cada grupo tomara sus datos solo dentro del laboratorio en un periodo corto de tiempo así uno por uno.
R/- La caída de los cuerpos se realiza con movimiento uniforme acelerado.
-Las cascadas de agua caen con movimiento uniforme acelerado.
-La velocidad del sonido es un movimiento uniforme.
-La velocidad de la luz es un movimiento uniforme.
- Con la realización de este laboratorio, se afianzó mediante la aplicación, los conceptos del movimiento uniforme y sus características al igual para el movimiento uniformemente acelerado.
- Se comprobó experimentalmente la relación funcional entre el espacio recorrido y el tiempo, para un cuerpo que se mueve con movimiento uniforme.- Se demostró experimentalmente la relación funcional entre espacio recorrido y tiempo para un cuerpo con aceleración, comprobando la ecuación cinemática:

REFERENCIAS
[1] http://es.wikipedia.org/wiki/Sistema_inercial
[2]http://www.sc.ehu.es/sbweb/fisica/cinematica/rectilineo/rectilineo.htm
[3] Serway, R. Física Volumen 1. Editorial. McGraw Hill. 5edicion

Para graficar la velocidad en función del tiempo se calcula la velocidad con la ecuación:
 se utiliza esta ecuación del movimiento uniforme aunque el movimiento es acelerado por que se requiere la velocidad en un intervalo de de espacio muy pequeño que es la longitud del diafragma del deslizador equivalente a 0.100 m en le momento de pasar por el sensor óptico en este intervalo de tiempo tan pequeño la variación de la velocidad casi es nula lo que hace que el movimiento sea aproximadamente con velocidad constante por esto se hace esta aproximación.
se utiliza esta ecuación del movimiento uniforme aunque el movimiento es acelerado por que se requiere la velocidad en un intervalo de de espacio muy pequeño que es la longitud del diafragma del deslizador equivalente a 0.100 m en le momento de pasar por el sensor óptico en este intervalo de tiempo tan pequeño la variación de la velocidad casi es nula lo que hace que el movimiento sea aproximadamente con velocidad constante por esto se hace esta aproximación.Se utiliza el tiempo medido en modo 2

 Grafica 7: velocidad versus tiempo del deslizador con movimiento uniforme acelerado.
Grafica 7: velocidad versus tiempo del deslizador con movimiento uniforme acelerado.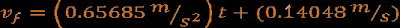
4. Con base en las graficas anteriores responda: ¿cómo se relacionan el espacio recorrido y el tiempo en le movimiento rectilíneo uniforme acelerado? ¿Qué significado tiene la pendiente de esta grafica? ¿Cómo se relaciona la velocidad y el tiempo en el movimiento rectilíneo uniforme acelerado? ¿Qué significado físico tiene la pendiente y el área bajo la curva de esta grafica?
R/ a) En la grafica de espacio versus tiempo se obtuvo una parábola lo que indican que estas magnitudes no son directamente proporcionales puesto que la pendiente de la grafica que es físicamente la velocidad no es una línea recta lo que indica que la velocidad varía respecto al tiempo y que lo hace de forma proporcional puesto que curva presenta que dicho movimiento se define matemáticamente con una ecuación de segundo grado:

que seria la ecuación de espacio que definiría dicho movimiento al derivar dicha ecuación se obtendría una ecuación lineal como la derivada de la ecuación de espacio da como resultado la ecuación de velocidad y es una ecuación lineal lo que indica que la velocidad es proporcional al tiempo en este movimiento.
b) La pendiente de esta grafica representa la velocidad del móvil el cual esta medida en m/s y va cambiando al transcurrir el tiempo lo que indica que hay una aceleración.
c) de la grafica 7 se puede deducir que la velocidad y el tiempo son dos magnitudes directamente proporcionales en el movimiento uniformemente acelerado lo que indica que al aumentar una la otra aumenta en al misma proporción.
d) La distancia (x) recorrida por el cuerpo desde el momento inicial hasta el momento (t) se puede obtener mediante el área bajo la grafica del velocidad versus tiempo, la ecuación:
 indica que la velocidad varia linealmente en el tiempo, este es el significado físico del área bajo la pendiente de la grafica velocidad versus tiempo. Matemáticamente:
indica que la velocidad varia linealmente en el tiempo, este es el significado físico del área bajo la pendiente de la grafica velocidad versus tiempo. Matemáticamente:
5. ¿Qué posible errores se cometieron en la realización del experimento y como los corregirías?
R/ Los errores se dieron porque los alumnos movían el riel de aire desnivelándolo, resultando discrepancia en los datos de tiempo tomados. Esto se corregiría si cada grupo tomara sus datos solo dentro del laboratorio en un periodo corto de tiempo así uno por uno.
6. De ejemplos de situaciones en los cuales se representan estos tipos de movimientos en la naturaleza.
R/- La caída de los cuerpos se realiza con movimiento uniforme acelerado.
-Las cascadas de agua caen con movimiento uniforme acelerado.
-La velocidad del sonido es un movimiento uniforme.
-La velocidad de la luz es un movimiento uniforme.
CONCLUCIONES
- Con la realización de este laboratorio, se afianzó mediante la aplicación, los conceptos del movimiento uniforme y sus características al igual para el movimiento uniformemente acelerado.
- Se comprobó experimentalmente la relación funcional entre el espacio recorrido y el tiempo, para un cuerpo que se mueve con movimiento uniforme.- Se demostró experimentalmente la relación funcional entre espacio recorrido y tiempo para un cuerpo con aceleración, comprobando la ecuación cinemática:

- Se estudio gráficamente el espacio en función del tiempo, la velocidad en función del tiempo, para el movimiento uniforme y para el movimiento uniformemente acelerado reconociendo sus características.
REFERENCIAS
[1] http://es.wikipedia.org/wiki/Sistema_inercial
[2]http://www.sc.ehu.es/sbweb/fisica/cinematica/rectilineo/rectilineo.htm
[3] Serway, R. Física Volumen 1. Editorial. McGraw Hill. 5edicion

